Anyone good at math?

[seven_deuce offsuit]

Ok, I know a lot of people don't like math and I don't like it as much either, but I am stuck on a problem and it's starting to bother me. In the problem, I'm suppose to find the first term (or a1) of a geometric series, and to help find it I am given this: Sn = 2457, an = 3072, and r = -4. After setting it up into two equations, I found that I might have to use both equations to solve a system or just one to solve for a1:

2457 = a1(-4^n-1)/-4-1 and/or 3072 = a1-4^(n-1)/-4-1.

I found the answer by randomly punching numbers into a calculator, but it won't be creditable if I don't show work, and that's where my problem lies.

[jimmalenko]

Ahhhh, the internet

Isn't this what your math teacher is for ?

[seven_deuce offsuit]

Yeah, but he only gave us one hint to solve it and that was to use a system. But I'm pretty sure there's more than one way to solve it.

[waheed]

Clue: make a1 the subject in both equations, and equal them with each other, this will eliminate a1 from the equations, then solves to find the value of n. After finding n, substitute back in and solved to find value for a1.

I think thats how to solve it. thats just a quick glance at the equations. Will need to look back into it. Haven't done maths since I left university (I did Engineering at uni)

[jimmalenko]

Haven't done maths since I left university (I did Engineering at uni)

Ditto

I coupled it up with Computing (Programming) though.

[northcat_8]

Ok, I know a lot of people don't like math and I don't like it as much either, but I am stuck on a problem and it's starting to bother me. In the problem, I'm suppose to find the first term (or a1) of a geometric series, and to help find it I am given this: Sn = 2457, an = 3072, and r = -4. After setting it up into two equations, I found that I might have to use both equations to solve a system or just one to solve for a1:

2457 = a1(-4^n-1)/-4-1 and/or 3072 = a1-4^(n-1)/-4-1.

I found the answer by randomly punching numbers into a calculator, but it won't be creditable if I don't show work, and that's where my problem lies.

I am confused by the syntax of your equation.

What is: 2457 = a1 (-4^n-1)/-4-1

[northcat_8]

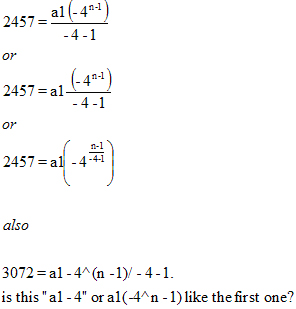
and could you just write out the equation with directions and let me set it up myself.

and solving it as a system of equations is going to be the easiest way to solve it, at least for me it will be.

Also, what class is it?

[e404pnf]

This is taking me back ... thought I'd always remember this

Anyway, aren't the first two the same?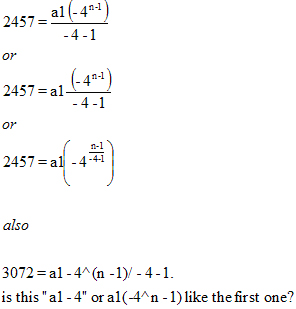

a   c     ac
- x -  =  --
b   d     bd

and the third would be written as 2457 = a1(-4^(n-1/-4-1))

[northcat_8]

Grrrrrrrr......yes they are...

In the second one I meant to put a subtraction sign between the a1 and the fraction.

[Cobra]

I saw this thread and instantly thought of Northcat.

[seven_deuce offsuit]

Ok, I know a lot of people don't like math and I don't like it as much either, but I am stuck on a problem and it's starting to bother me. In the problem, I'm suppose to find the first term (or a1) of a geometric series, and to help find it I am given this: Sn = 2457, an = 3072, and r = -4. After setting it up into two equations, I found that I might have to use both equations to solve a system or just one to solve for a1:

2457 = a1(-4^n-1)/-4-1 and/or 3072 = a1-4^(n-1)/-4-1.

I found the answer by randomly punching numbers into a calculator, but it won't be creditable if I don't show work, and that's where my problem lies.

I am confused by the syntax of your equation.

What is: 2457 = a1 (-4^n-1)/-4-1

It's suppose to be the first one and it's a1-4. This is for Algebra II by the way.

[lordsmurf]

I think I see the word "oral" in that last equation.

[seven_deuce offsuit]

and could you just write out the equation with directions and let me set it up myself.

and solving it as a system of equations is going to be the easiest way to solve it, at least for me it will be.

Also, what class is it?

(to the post above) lol, yeah I see it too. Anyway, the equation I plugged them into were

1. Sn = a1(r^n-1)/r-1, or read as: Sn = first term(common ratio to the n-1 power) all over common ratio minus 1

2. an = a1r^(n-1)/r-1, or read as: an = first term times the common ratio to the n-1 power all over the common ratio minus 1

And you are given these to solve for a1: Sn = 2457, an = 3072, and r = -4. At least I think those are the equations you need to solve it.

[ps2daddy]

You could graph both equations on the same graph and see where the points intersect and that would give you an answer to the problem (yaxis = a1 x axis =n)

or

like it was mentioned earlier represent one variable in terms of the other one and throw it in the other equation to get the other variable
(make it one equation with one unknown)

[northcat_8]

alright...I'll get to work on it, but a hint incase you check this before I post the work....you could solve one equation for a1, then substitute it in for a1 in the 2nd equation..."substitution method" instead of the "systems method".

[northcat_8]

first...your equations are wrong.

[northcat_8]

my last post is enough to figure out the problem.

my algebra 2 books and stuff are at school, so you'll have to wait until monday for a clinical "math teacher" explanation. How I see it in my own language is probably not going to be clear enough for you to understand.

Oh and by the way I absolutely hated Geometric finite and infinite series, thanks for making me re-familiarize myself with that crap

[seven_deuce offsuit]

first...your equations are wrong.

My math teacher said that the first formula I had are the same as the ones you posted, but I probably got the denominator mixed up. Although I may have to double check on that equation I used, but I can't right now because I left my stuff in my friend's car. As for my second equation, since I don't know how to write mathematical equations (i.e. square roots, subscripts, and so forth) using this message board, it may come out incorrectly. But the second equation you wrote on your second set of formulas is exactly what I meant. Yeah, if I knew how to write it like that, it probably would cause less confusion.

Oh and by the way I absolutely hated Geometric finite and infinite series, thanks for making me re-familiarize myself with that crap

lol, I don't know if I should say "you're welcome" or "sorry"