Does anyone here have knowledge of statistics?
The reason I ask is that I am currently doing a statistics course for university and was wondering if anyone could help me out with the following problem.
My logic would say that the percentage of 3 or more being booked is 0% seeing that only 10 cars pass through and the percentage of speeders is 28% therefore every 2.8 cars is a speeder.On the Ipswich Motorway near the Warrego Highway turnoff, it is
known that 28% of vehicles exceed the 80 km/h speed limit. If 10
vehicles pass a hidden police camera, what is the probability that
more than three will be booked for speeding? Give your answer
correct to four decimal places.
What do you think? Perhaps if I rounded it up?
+ Reply to Thread
Results 1 to 25 of 25
-
-
GuestGuestYou have two criteria. More than 3 and 3 or more.Originally Posted by pacmania_2001
-
You need to define your confidence level (in percentage) and you need to have a larger sample size to develop any kind of realistic confidence.
Boy this is dredging up bad memories from college statistics :P -
in my area -- everyone would be a speeder

also "booked for speeding" doesnt tell you squat about at what level you will get booked -- 1 mph over , 2 mph over etc ..
i always bitched about these problems .."Each problem that I solved became a rule which served afterwards to solve other problems." - Rene Descartes (1596-1650) -
It's not 2.8 cars out of every 10, but an average of 2.8 cars out of every 10. The "answer to 4 decimal places" was a clue to solving this problem, since this means 6 sigma confidence level (or 99.9999% level), IIRC. Look up computing confidence levels in your textbook. You'll find that the probability of getting 4 vehicles (or more) is around 20-30%.
Or something like that!ICBM target coordinates:
26° 14' 10.16"N -- 80° 16' 0.91"W -
You logic is flawed pacmania. It would seem that way but it is not.
while 28% indicates that no 3 cars in a group of 10 would all be speeding it is certainly a possibility and it is that possibility that you are seeking. So basically you are looking for "probability that 3 of those cars would be in that 10.what is the probability that
more than three will be booked for speeding?
I don't have time to explain all of this right now...I just found it and I have to leave, I will check back later.
Also the correct answer for your class is dependant on what you are doing in class. Probability obviously, but is it permutations and combinations, simple probability, experimental, empirical....you know, what "chapter" are you in so to speak.
I'll be back around 5:00 EST.
PS - I hated statistics
-
My mistake, what is quoted is correct. More than 3 cars being booked is the correct criteria.Originally Posted by Dr.Gee
I too thought the sample size was too small for it to be realistic.Originally Posted by Capmaster
Seeing you are only told 28% are speeding so I would assume it doesn't worry about that as such.Originally Posted by BJ_M
In real life we are allowed 10% plus/minus on the posted speed limit.
Thanks for the tip, I'll investigate more down that path.Originally Posted by SLK001
*Dives into textbook*
Ah ok, I'll probably still be no closer to an answer when you get back but I should be able to narrow it down to the field.Originally Posted by northcat_8
Look forward to your posts.
PS - I hated statisticsi always bitched about these problems .My sentiments exactly.Boy this is dredging up bad memories from college statistics
The class is Quantitative Economic and Business Analysis A and unfortunately for me is a required class for my degree. Last year they had only a 40% pass rate so I'm hoping to pass it first time and begone with it forever.
Thanks all for the help.
-
OK, now I will confess my statistics is very very rusty...8 years worth of rust.....But lets go this way....
Since the speeding and cars stopped are mutually exclusive events. The probability of the "UNION" of both circumstances. Therefore P(A U B) = P(A) + P(B).
Now it would be nice if we could just say...well that would be 3 out of 28, and 10 out of 100, do some arithmetic and be done...but alas, that is not the case.
Lets rewrite the problem so it's more comfortable for me. From a group of 28 speeding cars and 72 non-speeding cars, 10 cars are going to be selected at random. What is the probability that 3 or more speeding cars are selected.
OK, now there are no stipulations on which of the 28 cars are selected...making this a combination problem!!!!!!
In case you were sleeping in class...combination is ---> n! / r!(n-r)! or if you have TI-86 calculator it is ..... 2nd > math > prob and will be the "F3" key nCr....if you don't have a TI-82,83,85,86,89 or 92 calculator...sucks to be you, have fun with the arithmetic
Anyway...to the problem...
Now we have some situations here, first we need to determine the probability of if being exactly 3 cars. We will call this P(M), then we will need to determine the prob. if all 10 are speeders and we will call this P(N). Because remember we just have to have more than 3...so "3" is a minimum and 10 would be the max.
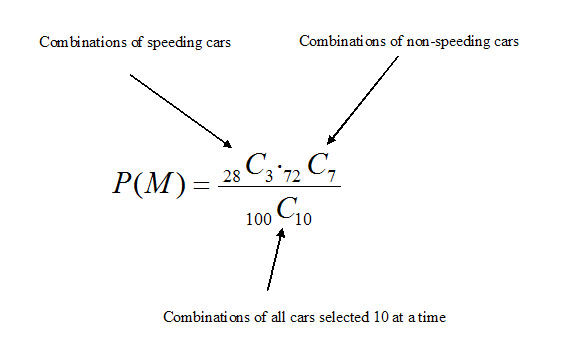
we will follow this same process for the P(N).
So the combination in the picture comes out to be:
P(M) = .278788048385
P(N) would be done a little different as we now do not have any that are NON-speeders in the mix. So our combinations would be (28 C 10) / (100 C 10)
P(N) = 7.58109497293 x 10^-7
 or --> .00000075810.....
or --> .00000075810.....
So the Probability of P(M U N) = P(M) + P(N) which is .278788048385 + .00000075810 = .278788806495
WHICH as you can see is very close to 28%...but is not 28% and would be counted wrong because statistics professors are loser bastards who are WAY to anal about the accuracy of the work. -
Thanks for that Northcat_8.



Now I just have to adapt that method for more than 3, instead of 3 or more. -
There is probably a blindingly obvious question but I suck at anything to do with statistics so here goes.

-
GuestGuest
Ok.Problem solved. I have one of my own. 15 out of 15 of my girlfriend's home pregnacy tests were positive. These are 99.8% accurate. What are the chances of the next one being positive?

-
i would put money on it ..
congrat's (i hope)"Each problem that I solved became a rule which served afterwards to solve other problems." - Rene Descartes (1596-1650) -
No that wouldn't change to a 4.Originally Posted by pacmania_2001
3 is a minimum....the question reads "more than three" ...that means anything greater than 3.
3.1
3.000000000000001
The problem that you are having with it is that you know what a car is and you know you can't have 3.1 cars on the road....statistics does not recognize that. You have to have AT LEAST 3 to satisfy the conditions of the statement.
P(M) = Probability of 3 cars = .278788048385
P(N) = Probability of 10 cars = .00000075810
What we have found with the P(M) is the probability that exactly 3 cars that are stopped will be speeding....the P(N) is the probability of all 10 cars stopped will be speeding. Notice how the P(M) is almost 28% and the P(N) is so small? The range between the two is the probability of them being over 3 cars.
SOOO...you were asleep?In case you were sleeping in class...combination is ---> n! / r!(n-r)! or if you have TI-86 calculator it is ..... 2nd > math > prob and will be the "F3" key nCr
The combinations are written n C r
P(M) that I attached.
n = 28
r = 3
So from the long equation I wrote above n! / r!(n-r)!, you would have
28! / 3!(28-3)! = 28! / 3!25!
Remember now "!" means factorial. Which means --> 5! = 5 x 4 x 3 x 2 x 1 = 120.
So 28! = 28 x 27 x 26 x 25 x 24 x 23 x 22 x 21 x 20 x 19 x 18 x 17 x 16 x 15 x 14 x 13 x 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
Which equals: 3.04888344612 x 10^29
304,888,344,612,000,000,000,000,000,000
which is $5.00 short of Bill Gates' net worth

I sure hope you have a graphing calculator

I also hope this is how you were suppose to do the problem...there are about 100 ways to do it depending on what part of statistics you are dealing with. -
Not so much asleep, its more of a trance I go into when anything statistical is mentioned.SOOO...you were asleep?
Thanks again for the help.
Congrats Dr.Gee (if its good news). -
GuestGuest
How come they never have EPT commercials where there is a guy pacing a room,distraught, pulling out his hair,saying "Oh shit,man!, now what?"

-
The probability of MORE than 3
= 1 - (P(0) + P(1) + P(2) + P(3))
P(0) = probability of 0 cars over speed limit
P(1) = probability of 1 car over speed limit
P(2) = probability of 2 cars over speed limit
P(3) = probability of 3 cars over speed limit
Note: the answers below are rounded for presentation but not in the actual calculation...
The probability of EXACTLY 0 cars over the speed limit (out of 10) is:
P(0) = (0.28)^0 * (0.72)^10 * 10C0
P(0) = 1 * 0.0374 * 1
P(0) = 0.037
The probability of EXACTLY 1 car over the speed limit (out of 10) is:
P(1) = (0.28)^1 * (0.72)^9 * 10C1
P(1) = 0.28 * 0.0520 * 10
P(1) = 0.146
The probability of EXACTLY 2 cars over the speed limit (out of 10) is:
P(2) = (0.28)^2 * (0.72)^8 * 10C2
P(2) = 0.0784 * 0.0722 * 45
P(2) = 0.255
The probability of EXACTLY 3 cars over the speed limit (out of 10) is:
P(3) = (0.28)^3 * (0.72)^7 * 10C3
P(3) = 0.0220 * 0.1003 * 120
P(3) = 0.264
Thus, the probability of MORE THAN 3 cars out of 10 being over the speed limit is...
1 - (0.037 + 0.146 + 0.255 + 0.264)
= 0.29794054440003567616
~ 0.2979
Or: 29.79%
The above method can be simply worked out with a normal calculator... ;-)
Regards.Michael Tam
w: Morsels of Evidence -
There is a 3.2768 * 10^-39 percent chance that your girlfriend is NOT pregnant.Originally Posted by Dr.Gee
That is 0.0000000000000000000000000000000000000032768 %
For all intents and purposes, the chance that the next test will be positive is 99.8% (i.e., the accuracy of the test).
Best regards. Michael Tam
Michael Tam
w: Morsels of Evidence -
Thanks for all the replies but now I have another statistic related question for you.
The question is:
To work this out would you use the formula?Suppose that the probability that tomorrow will be a rainy day is
0.20 and the probability of it being windy tomorrow is 0.29. If the
probability that it will rain and be windy tomorrow is 0.07, what is
the probability it will be windy or rainy or both tomorrow? Give
your answer correct to two decimal places.
P(A or B or [A+B])=P(A)+P(B)+P(A + B)
A = Rain
B = Wind
C = Both Wind and Rain
Cheers. -
I think that question is implying that the probability of rain and wind are NOT independent of each other... otherwise, the chance of wind AND rain would be: 0.20 * 0.29 = 0.058 (rather than 0.07). In any case, this is a red herring in the question and is irrelevant.
OR in statistics means "+"
AND means "*"
So:
P(answer) = P(rain) + P(wind) + P(rain + wind)
= 0.20 + 0.29 + 0.07
= 0.56
Best regards.Michael Tam
w: Morsels of Evidence -
I don't have time to elaborate on this right now...this stupid "work" thing is getting in the way.
Probability of Mutually Exclusive Events:
The probability of one or th eother of two mutually exclusive events, A and B, occuring is the sum of their probabilities.
P(A or B) = P(A)+P(B)
Probability of Inclusive Events:
The probability of one or the other of two inclusive events, A and B, occuring is the sum of the individual probabilities decreased by the probability of both occuring.
P(A or B) = P(A) + P(B) - P(A and B) -
Thanks all for the help.
The test didn't go too smoothly but I'll get over it. As long as it's enough to pass the subject so I can forget anything stats related for the rest of my life. -
what's the chance of that ?
"Each problem that I solved became a rule which served afterwards to solve other problems." - Rene Descartes (1596-1650) -
Originally Posted by BJ_M

I am hoping for a 4 (Pass) but would be happy with a 3 (Conceded Pass). -
Statistically speaking, it may come down to how well he kisses ass...Originally Posted by BJ_M

-
Thanks to standardised central testing kissing arse is no longer a variable in the situation.Originally Posted by indolikaa

Similar Threads
-
Program To Display VIDEO Statistics
By u100h in forum ComputerReplies: 0Last Post: 3rd Aug 2011, 18:17 -
iPod last.fm-type statistics program (total songs played in last week, etc)
By Salva Veritate in forum Portable VideoReplies: 0Last Post: 22nd Jan 2009, 16:54



 Quote
Quote