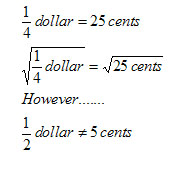3 man puzzle.
If the front 2 men had on black hats then the 3rd guy would have known immediately since there were only 2 black hats. Since he didn't guess, the man in the middle knows that he and the front guy either have 2 whites, or 1 black and 1 white. If the front guy had a black hat then the 2nd guy would know he had a white hat. Since the second guy didn't guess, the 1st guy knows that he has on a white hat. Either he and the 2nd guy both have on white or he has on white and the 2nd guy has on black. Either way, the guy closest to the wall knows he's wearing white.
+ Reply to Thread
Results 121 to 150 of 376
-
-
My thinking is that if the pencil swaps ends, then there's some kinda twisting motion involved (as with my original solution).Originally Posted by thecoalman
So, having re-thought it, I think I've cracked it (again):
1. Start as stated.
2. Cross thumbs, with right thumb uppermost (I'm right-handed).
3. Bring the right hand's fingers in towards the centre and over the pencil and the fingers of the left hand (with the left hand's fingers coming in too).
4. Half way through, you have the thumbs interlocked with the pencil sandwiched betwen them.
5. Continue with a twisting motion whereby the skin between the index finger and thumb on each hand rub against each other, et volia!There is some corner of a foreign field that is forever England: Telstra Stadium, Sydney, 22/11/2003.
Carpe diem.
If you're not living on the edge, you're taking up too much room. -
i had just come up with the same solution, here!
http://www.geocities.com/flaninacupboard/hands.htm -
GuestGuest
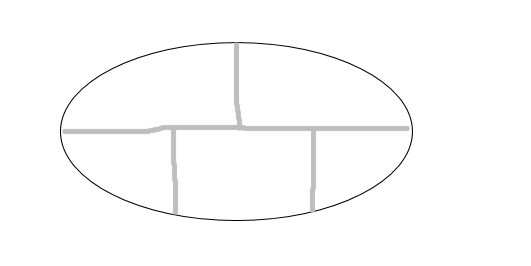
Here's an unsolvable puzzle that is useful if you need to keep someone busy or you are just plain sadistic. You draw the first figure. You then try to draw one continuous line (red,2nd figure) that goes thru every grey section once and only once. You can always get it down to one remaining.
I spent hours trying to figure this one out as a kid. Our 5th grade teacher had a $5 prize for whomever could solve it. Bastard! He gave me a dollar when I told him I researched it and found it unsolvable. Hush money indeed
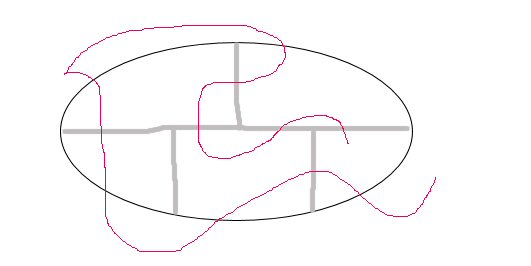
-
Dr Gee,Originally Posted by Dr.Gee
Please correct me if Im wrong, but in your second diagram, if you move the red line in the lower, left quadrant up by about 1.5 cm then you will have crossed each grey section. I'm sure I'm missing something here, are there any more rules?
Cheers
Ironballs -
GuestGuestOriginally Posted by Ironballs
Lazy on the diagram. This includes the oval perimeter. Actually, this is the actual diag.
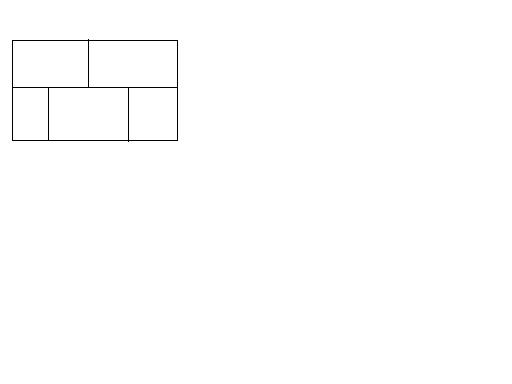
-
Adam wrote
Excellent that's the solution. Hope you solved it yourself and didn't already know the answer. As you figured, the guy in front can only know if he imagines what his friends can see.3 man puzzle.
If the front 2 men had on black hats then the 3rd guy would have known immediately since there were only 2 black hats. Since he didn't guess, the man in the middle knows that he and the front guy either have 2 whites, or 1 black and 1 white. If the front guy had a black hat then the 2nd guy would know he had a white hat. Since the second guy didn't guess, the 1st guy knows that he has on a white hat. Either he and the 2nd guy both have on white or he has on white and the 2nd guy has on black. Either way, the guy closest to the wall knows he's wearing white.
Credit also goes to northcat_8 who pm'd me with the answer since he already uses this puzzle in his classes. -
Not valid?? 1/4 of a dollar does equal 25 cents, just like 12 inches = 1 foot, or 100 cm = 1 meter.Originally Posted by Ironballs
You are correct in your thinking though. The issues comes with trying to use mathematical operations on 2 equal quantities in different units. -
Originally Posted by Dr.Gee


 Good Ol' Euler and those crazy paths of his...
Good Ol' Euler and those crazy paths of his...  ...apparently not many math majors out there.....
...apparently not many math majors out there.....
-
Actually the error is in between the second and third line. You cannot simply remove the "dollars" and "cents" out of the square root. The final line should actually read:Originally Posted by northcat_8
1/2 "root dollars" = 5 "root cents" -
This puzzle may or may not be solvable. The version I am presenting here is solvable because I omit 1 thing.
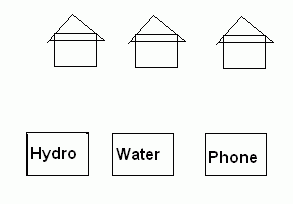
You must connect each service to each house by a solid line but it does not have to be straight. Each line can only go to one house and you must not cross any of your lines nor go through any other house to bring the service in. Have fun!
-
Daamon,
Sounds like you have it, particularly where you state that you cross your thumbs. Flaninacupboard I wasn't able to open your movie. As long as the pecil never leaves the crook of your thumbs you did it. I'm pretty sure there's only one way to do it. -
Which is using a mathematical operation on quantities of different units. Which will always yield skewed results.Originally Posted by SquirrelDip
You could do the same thing with inches and feet.
1/4 sq. foot = 6 sq. inches
or anything of different units.
-
Originally Posted by northcat_8
However:
1/4 sq. foot = 36 sq. inches (not 6 sq. inches)
Take the root of both sides and you have 1/2 foot = 6 inches (true)...
(I knew that dimensional analysis course would pay off one day...)
But, in your defence you have valid point when the "zero" is not common: for example when comparing degrees fahrenheit to degrees celcius... -
Couldn't play it. I used windows media player, said unknown error. I just tried opening it in my video editor says no combination of intermediate filters... I downloaded it directly to my comp, do i need to stream it or something.Originally Posted by flaninacupboard
-
1/4 sq. foot = 6 sq. inches
 should be 1/4 foot^2 = 36 in^2
should be 1/4 foot^2 = 36 in^2
This last example is only possible because of the units being squared, which allows you to square root both the number and the unit, if it were changed to be
1/4 ft = 3 inches
then take the square root of both sides, you end up with
1/2 ft = radical 3 inches
which is not true because you are dealing in linear units.
The answer to the original post is:
The logic of the problem is sound. And operations are legal. The problem becomes illogical in the end because of the difference in the units of measure.
It is an illustration in the importance of having like units before working with quantities under mathematical operations. -
@northcat_8: I see we're not going to come to an agreement on this topic

You took the square root of 1/4 ft^2 and got 1/2 foot (which I agree) but you then take the square root of (1/4 foot) and get 1/2 foot??? Why does it follow that when taking roots it's okay to reduce the exponent from foot^2 to foot but not foot to foot^0.5??? -
HOUSEKEEPING:
Still outstanding (in order of posting) - as best I can see:
Marbles in a Bath - Solved
Fairground Worker - Solved
Large Island, Dodgy Natives - Solved
Services and Houses - Answer Provided
Rules / Guidelines
Of course, you don't have to follow these rules, coz I'm not Baldrick - but it'd help.There is some corner of a foreign field that is forever England: Telstra Stadium, Sydney, 22/11/2003.
Carpe diem.
If you're not living on the edge, you're taking up too much room. -
Who owns the zebra?
This is an old one also which I had to look for on the net. The solution is also posted on the net so please do not do any searches. It takes a while to solve but it's all logic. The solution can be found by using the information provided.
Who owns the Zebra?
Based on the clues listed below
============================
There are five houses.
Each house has its own unique color.
All house owners are of different nationalities.
They all have different pets.
They all drink different drinks.
They all smoke different cigarettes.
The English man lives in the red house.
The Swede has a dog.
The Dane drinks tea.
The green house is on the left side of the white house.
They drink coffee in the green house.
The man who smokes Pall Mall has birds.
In the yellow house they smoke Dunhill.
In the middle house they drink milk.
The Norwegian lives in the first house.
The man who smokes Blend lives in the house next to the house with cats.
In the house next to the house where they have a horse, they smoke Dunhill.
The man who smokes Blue Master drinks beer.
The German smokes Prince.
The Norwegian lives next to the blue house.
They drink water in the house next to the house where they smoke Blend.
So, who owns the Zebra?
==============================
Enjoy! -
How long is a foot^.5?? What common unit of measure would that be called? Inches? radical feet?Originally Posted by SquirrelDip
It doesn't follow....it's not suppose too, that's the point of this thread and that's why I said...
"It is an illustration in the importance of having like units before working with quantities under mathematical operations."
The posts in this thread only appear to be mathematically logical...read the first mathematical post where "a=b".... where the person appeared to have a logical process only to come out with 2=1 or something like that. They got this result by dividing my zero...which is undefined...hence the purpose of the thread.
We don't have to agree...If you want the clinical explanation:
Most people recall the axioms, or assumptions, which are at the foundation of the study of arithmetic and which are consequently essential to any mathematical argument having to do with numbers. Most probably remember them in some fashion as: "Equals plus or equals minus equals are equal;equals times or divided by equals are equal; like powers or like roots of equals are equal; things equal to the same thing are equal to eachother; etc" (basically saying what you do to one side of a equality you must do to the other side and the equality will remain equal.) The previous descriptions are more how people remember the properties rather than me describing them as the transitive property, or the multiplication property of equality.
The problem I posted is a misapplication of these axioms....meaning, when you start out with 1/4 dollar = 25 cents...that is a true statement...by the rules of algebra you can apply the same operation to both sides of the equation and the equation will remain equal...however, in this case...it does not. And the reason it does not is because of the units...if you make the 25 cents, .25 dollars everything is just fine and the equations remain equal. The steps are algebraically sound but the answer is not logical....and that's why I posted it in this thread.
-
You're missing the point - the actual dimensions are meaningless. How long is a ft^0.5, who cares, how long is a square foot? - Just as meaningless. Imagine outside the 3d world where ft^0.5 exist as well as, say, ft^4Originally Posted by northcat_8
My point is that the square root of (A * B) = square root (A) * square root (B). You can't simply relax this rule because ft^0.5 can't be measued with a stick - this is like saying that the square root of 2 doesn't exist because you can't exactly represent it as a decimal.
Is there anyone else out there that can take a stab at explaining this??? Or, anyone that can else that can explain northcat_8's point to me??? -
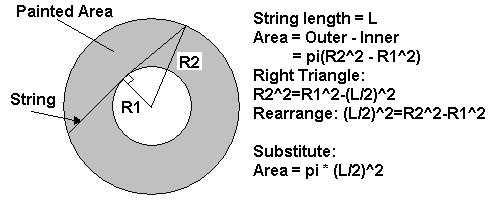
In essence, correct - except that you state R2^2 = R1^2 - (L/2)^2, when in fact it should be plus (from Pythagoras Theorem), but I'll take that as a typo as the re-arrangement is correct.Originally Posted by SquirrelDip
Well done, I was stumped for ages on that one!
Having followed the heated debate (with a grin, admittedly), I'd have to say that northcat_8 is correct, as is SquirrelDip - it's just that you're not quite connecting with each other.Originally Posted by SquirrelDip
I'll try to summarise but, first of all, forget all that has gone on before - start afresh.
1. The first line is a statement of truth, represented mathematically. Before any operations can be done, the units on each side have to be the same. This is where the misleading begins...
2. The problem lies with the second line, where the square root is first introduced.
3. The algebraic logic in that line is correct - apply a mathematical function (square root in this case) to both sides of the equation and all is still equal. Except in this case, the units are still different - so the logic is OK, but it's going against a different rule of maths (see point 1).
4. northcat_8's point is that, before performing any mathematical operation, the units on each side have to be the same otherwise the numbers involved are meaningless. That's maths - it's the law.
5. The third line then goes on to complete the misdirection by applying the square root just to the numbers, and then sticking the units on to make the untruth seem achievable - all because of the flaws mentioned above.
As northcat_8 has said, it's the same principle as the first problem posed where 2 ends up equalling 1 - the logic was correct, but a different rule of maths was violated (dividing by zero in that case). Same here, different puzzle, different rules violated.
Hope that helps SquirrelDip...There is some corner of a foreign field that is forever England: Telstra Stadium, Sydney, 22/11/2003.
Carpe diem.
If you're not living on the edge, you're taking up too much room. -
Without the units the original statement would not be true in the first place....Originally Posted by SquirrelDip
1/4 dollar = 25 cents
but
1/4 does not equal 25.
I understand what you are saying, I am familiar with mathematical operations and everything else you said. It is important that you be able to state it in terms that can be used. True it can't just be dismissed, but if I am due change back you have to be able to return "dollar^.5" unit of money.
Not worth arguing over. There's the problem, I gave the answer that Dr. Zill wrote in the Paradox book I got it from back in the day, if you don't agree with it...take it up with Dr. Zill. -
 Beep, beep, beep... Paging Dr. Zill, paging Dr. Zill...
Beep, beep, beep... Paging Dr. Zill, paging Dr. Zill...
Here's a paradox:
Take a sheet of paper, write on it: "Everything statement written on this paper is incorrect."
If the statement is true then the statement must be false, but if the statement is false then the statement must be true.
(Russell's Paradox) -
Some know this some do not...
But you cannot fold a single piece of paper in half more than 8 times by hand.
Try it.
I've made $3.75 in 3 periods today (.25 a try) kids are so easy
(.25 a try) kids are so easy 
-
Here's an old one...
The Missing Dollar:
Three nearly broke college men on their way to spring break stop at a motel for the night. The cashier tells them a room is $30. They each put in $10. Later, the manager tells the cashier the room should have only been $25, so the manager gives the cashier five $1 bills to return to the men. Not knowing how to divide $5 among three men, the cashier gives $1 back to each man and keeps the other $2 for himself. This meant that the three men each paid $9 for the room, which is a total of $27. Add the $2 that the cashier kept and you have $29. What happened to the other dollar? -
From page 1 of this thread:Originally Posted by SquirrelDip
https://www.videohelp.com/forum/viewtopic.php?p=897226#897226
Sorry...There is some corner of a foreign field that is forever England: Telstra Stadium, Sydney, 22/11/2003.
Carpe diem.
If you're not living on the edge, you're taking up too much room.
Similar Threads
-
Can you solve this puzzle?
By tin2tin in forum Newbie / General discussionsReplies: 8Last Post: 15th Apr 2012, 23:54 -
VirtualDub filter to insert video from another source into a corner?
By Riothamus in forum EditingReplies: 2Last Post: 6th Jun 2011, 08:51 -
Picture looks like a puzzle of 1000s of small blocks
By Twheels in forum Authoring (DVD)Replies: 5Last Post: 4th Sep 2009, 13:58 -
Vobsub causing pixelation on upper RH corner?
By Uzysuicide in forum SubtitleReplies: 2Last Post: 7th Feb 2008, 18:13 -
Puzzle of Camstudio AVIs
By terrypin in forum Newbie / General discussionsReplies: 2Last Post: 7th Dec 2007, 16:01




 Quote
Quote